爱因斯坦有一句话很深刻,他说:“逻辑将引领你从A到Z,想象力引领你到任何地方。”
在华老《高等数学引论》这本书里,在他整个教学过程中,逻辑联系的紧密程度和想象力空间的广阔,都是非常鲜明突出的。
华老,他精心给我们安排的这些教学内容,不仅颗颗都是发光的“珍珠”,而且经过他巧妙的安排,将这些“珍珠”连接成一串,构成一个有机的智慧整体。
印度诗人泰戈尔说:你可以把花瓣摘下,却拼接不出花朵的美丽。(You took off the
petals,but you do not gather the beauty of the
flower。)
华龙这个数学体系却将孤立的花瓣拼接出了“花朵的美丽”。它的魅力不仅体现在“花瓣”间严密的逻辑关系,而且在想象力上,同时开拓了一大片广阔的天空。让我们身在其中,延绵不断,反复品味它的学术甘香。
例如,华老对四元数的处理,就非同一般。
在他开始讲授这门课的时候,就给我们介绍了“四元数”。恕我孤陋寡闻,我真没看到哪些同类教本是这样处理的。
开始,我们对四元数也并不介意,因为华老对此也是点到为止。可是之后,我们慢慢体会到,华老这样安排,旨在为我们留下一条路,待以后再踏上它的时候,
就会看到完全不同的一番景观。正如英国诗人Frost那首影响很大的诗歌“ The Road Not
Taken” 所描述的那样。
形式上四元数似乎是复数的拓展,其实在我们探索分析时,华老至少给我们暗地里铺就了一条代数的路径。
我们知道,分析改变着我们的思维,而代数则在改变我们思维的同时,也提供了“操作式”的路径,后者往往是可触摸的,可运作的。
不仅如此,后来我才发现,引进四元数的W.Hamilton,在发现四元数的过程中还带有很重要的“创造性思维”特征。
美国著名科普作家Martin Gardner有一套“aha”丛书,影响很大。在其中一本叫
《aha, In sight(啊哈,原来如此)》的书中,就有关于四元数的精彩描述。Hamilton对四元数苦思冥想得不到解决,突然有一天灵感骤然从脑海中飞出,他就立即就把结果刻印在都柏林运河边上的一座小石桥上,…….。
再后来,当我们在决策学中碰到对H.Simon的决策范式时,感到他的“理性有限论”说的不够透彻,也没有说到根本问题上。正是“四元数”连带着的发现历史和思维特征,引发了我们对Simon决策学派加以重新审视。
第二、在《引论》中的有一个很厉害的“幽灵”,它就是“算法幽灵”
《共产党宣言》开篇第一句:“一个幽灵,一个共产主义的幽灵在欧洲徘徊,……”。后来这个幽灵,改变了世界,并且正在继续改变着世界。
华老的教育体系中也有一个“幽灵”,已经改了世界,并且正在继续改变着世界,那就是算法
–algorithm。我之所以将算法比作“幽灵”,因为华老当时并没有用这个术语。
可以这样说,当今世界,算法支撑着人类社会的几乎所有活动,并改变着人类的存在方式。从粒子加速器到股市,从观看新闻到搜索知识,从写文章到画图,从购物到旅游,等等,无不都与算法密切相关。
毫不夸张地说:算法就是笼罩着信息社会一个很厉害的“幽灵”。
然而,在60年前,华老已经悄悄地将算法介绍给我们。
华老以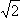 为例,令其分数部分ξ = 为例,令其分数部分ξ =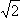 -1,容易建立关系式
ξ = -1,容易建立关系式
ξ = 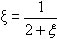 。 。
基于上面的等式,右边的分式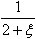 ,让分母的ξ取值从0开始,取得近似值 ,让分母的ξ取值从0开始,取得近似值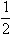 ;再让ξ取值 ;再让ξ取值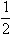 ,并得到另一近似值
,并得到另一近似值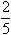 ;……这样一步步地往下深探,便可以按照一“盈”一“亏”的近似方式得到了ξ的近似值。
;……这样一步步地往下深探,便可以按照一“盈”一“亏”的近似方式得到了ξ的近似值。
华老这样讲授,极好理解,看似起点很低,然而其中内涵却极其丰富,有如“一石多鸟”:
其一,让我们脑子里建立起一个很生动的“无穷逼近”的坚实样板。
其二,基于此,华老引进了实数的特殊的建立方式。
其三,就算发而言,这是典型的“迭代法”,一种可以用计算机实现的最早算法。
这样的例子在《引论》中还有很多,华老在讲微积分正题之前,还专门给我们讲授了二进制计算、误差理论、Lagrange
插入公式、Newton 插入公式等这些早年算法的构造原理。
作为系主任,华老独具慧眼地把我们系的名称定为“应用数学与计算机技术系”,华老超前的学术眼光是非常了不起的。
也就是说,华老的卓越贡献不仅表现在数学上,也表现在建立计算机的贡献上。他不仅对我国计算机的起步贡献很大,而且对算法,这类极其重要的软件内核的贡献也是非常突出的、非常前沿的。
对此,我曾经认真考虑过,华老的这些思维结构,其源头出自于什么地方呢?
这让我想到,维纳三十年代访问清华,在华老与维纳交往将近一年。在这个过程中,维纳对华老不仅很欣赏,而且在华老出国留学等方面都给予关键性的帮助。维纳,他不仅是控制论的开创者,而且在信息科学方面,也是和先农可以比肩的重要奠基人,。
因此从这视角,对华龙体系进行延伸性的探索,也是很有意义的。
因为科学是无国界的,清华大学,以及后来的剑桥大学的学术平台等,都为华老敏锐地吸收最前沿的科学知识提供了珍贵的源泉。
我们纪念华老,发扬“华龙”精神,不能忘记这一点。
第三,是华老在文理结合上功夫很深,为我们提供了文理结合的样板,其前景同样是一片广阔的天地
在我们刚入学那一年,华老就在人民日报上撰文“大哉,数学之惟用!”。在《引论》书中,诸如“急就章”此类半文半白的词语时时跳入我们的眼帘。
华老的文章佳美,往往文中带诗,阅读起来,令人心旷神怡,思绪洞开。
华老在《引论》中曾引用老庄的哲学思想,他在书中说:“我国古代早就有了这一概念的萌芽,‘一尺之棰(书中原文为“槌”),日取其半,万世不竭’就是极限的看法。”
华老这样的言教身传,让我们班的许多同学,包括我在内,养成了注意关注中华国粹文化的习惯。难怪有中国学者这样说,搞自然科学的人,是不能不读老庄哲学的。
远的不说,就说庄周梦蝶的故事,它所描述的“角色互换”的对称现象,在当今的信息社会不正愈来愈明显吗!
我觉得,“文理结合”的这个问题,其意义超出数学本身的教育问题,涉及到人才培养的知识结构问题,也关系到回应“钱学森之问”的大问题。因此,文理结合,也正是我前面说到的“拼接出花朵的美丽”的重要途径。
总而言之,华老的《引论》,连同华龙体系,乃是华老精心打造,长年坚持。它体现了整体的绚丽,具有广阔的延拓空间,其学术魅力光彩四射,并经得起时光的考验,成为了不朽的学术经典,连绵不断地绽放出智慧的光芒。
华老有一首“豆芽菜”诗:
同是一粒豆,两种前途在。
阴湿覆盖中,养成豆芽菜。
娇嫩盘中珍,聊供朵颐快。
如或落大地,雨润日光晒。
开花结豆荚,流传代复代。
春播一斛种,秋收千百袋。
华老在告诫我们,“种豆”是要“落大地”的,只有这样才可以演化出 “一斛”变成
“千百袋”的神奇。华老用诗化式的语言,抒发了华龙教育体系意欲打造神奇的情怀。
我坚信,华老所抒发的这种“通天塔”的高尚情怀,一定会一代一代传接下去,发扬光大。
最后祝福中国科大母校越办越好,东风永恒!
谢谢大家!
|